AND problems

• AND

Some bit manipulation problems require to use AND in code. In this article, I will introduce couple AND problems and solution. AND is represented by & in C language. AND truth table is shown below.

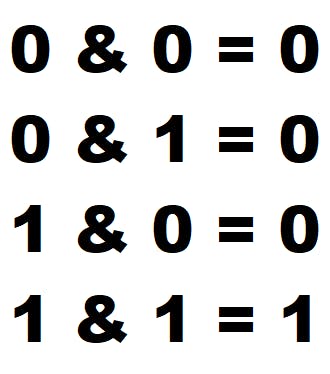
When two bits are 1, result is 1. Rests are 0.

• Problem1: Return number of 1s when given unsigned integer number is represented as binary. Reference:leetcode.com/problems/number-of-1-bits/solu..

uint32_t problem1(uint32_t input)
{
    uint32_t output = 0;
    //Implement logic

    return output;
}

Brute force approach would be looping through all bit and increase count if value is 1. Another approach would be repeat input = input & (input - 1) until input = 0. input & (input - 1) always flips the least significant 1-bit in input to 0. So, each iteration will find out 1 in current input.

• Implementation and test

1. Create and_problems ceedling project

   ceedling module:create[and_problems]
   

2. and_problems.h

   #ifndef AND_PROBLEMS_H
   #define AND_PROBLEMS_H
   #include <stdint.h>
   uint32_t problem1_1(uint32_t input);
   uint32_t problem1_2(uint32_t input);
   #endif // AND_PROBLEMS_H
   

3. and_problems.c

   #include "and_problems.h"
   uint32_t problem1_1(uint32_t input)
   {
    uint32_t output = 0;
   
    while(input != 0)
    {
        if(input % 2 == 1)
        {
            output++;
        }
        input /= 2;
    }
    return output;
   }
   uint32_t problem1_2(uint32_t input)
   {
    uint32_t output = 0;
   
    while(input != 0)
    {
        input = input & (input - 1);
        output++;
    }
    return output;
   }
   

4. test_and_problems.c

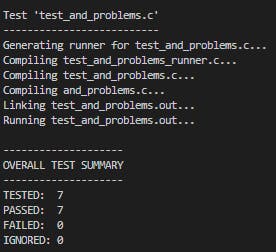
   #include "unity.h"
   #include "and_problems.h"
   void setUp(void)
   {
   }
   void tearDown(void)
   {
   }
   void test_and_problem1_example1(void)
   {
    TEST_ASSERT_EQUAL(2, problem1_1(5));
    TEST_ASSERT_EQUAL(2, problem1_2(5));
   }
   void test_and_problem1_example2(void)
   {
    TEST_ASSERT_EQUAL(0, problem1_1(0));
    TEST_ASSERT_EQUAL(0, problem1_2(0));
   }
   void test_and_problem1_example3(void)
   {
    TEST_ASSERT_EQUAL(32, problem1_1(0xFFFFFFFF));
    TEST_ASSERT_EQUAL(32, problem1_2(0xFFFFFFFF));
   }
   

5. Run test and result

   ceedling test:and_problems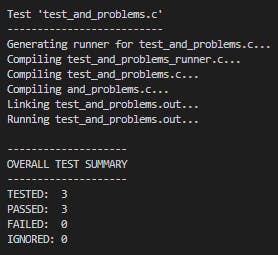
   

   

• Problem2: Given an integer n, return 1 if it is a power of two. Otherwise, return 0. Reference: leetcode.com/problems/power-of-two

  uint8_t problem2(uint32_t n)
  {
    uint8_t result = 0;
    //Implement the logic
  
    return result;
  }
  

• Implementation and test

Brute force approach would be iterate until n becomes 0 and each time checking if n modulo 2 is not 1 then divide up by 2 and continue. Another approach would be checking if n is equal to n & (-n) assuming n is not 0.

1. Add function prototype in and_problems.h

   uint8_t problem2_1(uint32_t n);
   uint8_t problem2_2(uint32_t n);
   

2. Add function in and_problems.c

   uint8_t problem2_1(uint32_t n)
   {
    uint8_t output = 1;
    if(n == 0)
    {
        output = 0;
    }
    else
    {
        while(n != 0)
        {
            if((n % 2 == 1) && (n != 1))
            {
                output = 0;
                break;
            }
            n /= 2;
        }
    }
    return output;
   }
   uint8_t problem2_2(uint32_t n)
   {   
    uint8_t output = 1;
    if(n == 0)
    {
        output = 0;
    }
    else
    {
        output = ((n & -n) == n) ? 1 : 0;
    }
   
    return output;
   }
   

3. Add test cases in test_and_problems.c

   void test_and_problem2_example1(void)
   {
    TEST_ASSERT_EQUAL(1, problem2_1(16));
    TEST_ASSERT_EQUAL(1, problem2_2(16));
   }
   void test_and_problem2_example2(void)
   {
    TEST_ASSERT_EQUAL(0, problem2_1(15));
    TEST_ASSERT_EQUAL(0, problem2_2(15));
   }
   void test_and_problem2_example3(void)
   {
    TEST_ASSERT_EQUAL(0, problem2_1(0));
    TEST_ASSERT_EQUAL(0, problem2_2(0));
   }
   void test_and_problem2_example4(void)
   {
    TEST_ASSERT_EQUAL(1, problem2_1(1));
    TEST_ASSERT_EQUAL(1, problem2_2(1));
   }
   

4. Run test and result

   ceedling test:and_problems